TEORÍA GENERAL DE LAS TURBOMÁQUINAS HIDRÁULICAS

El teorema de conservación de momento cinético puede proporcionar resultados muy útiles para el estudio teórico y el diseño de las turbomáquinas y de las instalaciones de bombeo y centrales hidráulicas. La fuerza del fluido sobre un conducto con cambio de dirección (codo) o cambios de sección obtenida por aplicación del mencionado principio determina el dimensionamiento de los apoyos necesarios en las conducciones. Cuando se aplica al fluido contenido en el rotor de la turbomáquina, se obtiene la ecuación fundamental de las turbomáquinas o Ecuación de Euler. Antes de su deducción, consideremos los casos básicos que se presentan a continuación.

Acción del fluido sobre los alabes 

Se busca en este punto la fuerza que un chorro de fluido ejerce sobre un alabe por aplicación de la ecuación de conservación de momento lineal en forma integral. Se considerarán tres casos: ´alabe fijo con respecto a un sistema de referencia fijo a tierra, ´alabe móvil a velocidad lineal constante con respecto a ese mismo sistema de referencia y finalmente, ´alabes montados sobre una rueda con rotación uniforme. En todos los casos el flujo puede suponerse incompresible y el movimiento relativo al ´alabe estacionario.

Alabe fijo 

Suponga que un chorro de fluido sale por una tobera a la atmosfera a velocidad →c1 medida con respecto a un sistema de referencia fijo a tierra, e incide sin disgregarse en régimen estacionario (hipótesis [1]) sobre un alabe fijo a tierra, como se muestra en la figura 2.12. El alabe desvía al chorro un ´Angulo θ y se asume la incompresibilidad del flujo (hipótesis [2]). Considere el volumen de control cerrado por la superficie S. Dicha superficie estará formada por las superficies S1, por la cual el fluido entra al álabe, S2, a través de la cual el flujo abandona el álabe, S3, que coincide con la entre cara de separación fluido-aire y S4, que es la superficie de contacto entre el fluido y el alabe. Se supondrá además que se pueden considerar propiedades uniformes en cualquier sección recta que atraviese el volumen de control (hipótesis [3]) y que el tensor de tensiones se reduce a las presiones en S1 y S2 (hipótesis [4]). Aplicando las ecuaciones de continuidad y de conservación de cantidad de movimiento al volumen de control definido, se tiene que:

• Ecuación de continuidad

Recordando la ecuación de continuidad en su forma más general se escribe que:

Se comprueba que esta ultima expresión se puede poner como:



siendo V un volumen fijo en el espacio, que en el instante considerado coincide con el volumen fluido Ve. Desarrollando cada uno de los términos de la ecuación 2.10, se puede escribir:



ya que solo existe flujo de fluido a través de las superficies S1 y S2 de la superficie de control.

El primer término del segundo miembro de 2.10 es la resultante de la fuerza de superficie que actúan sobre la superficie de control. Haciendo uso de la hipótesis [4], dicho termino adopta la forma:

y la expresi´on 2.12 se reduce a:

El ´ultimo término de la ecuación 2.10 cuantifica el efecto de las fuerzas de volumen que act´uan sobre el volumen de control. Al ser un sistema de referencia inercial, no existen fuerzas de inercia. Sí sería necesario incluir en este término el peso del volumen de control, que como se ha dicho, coincide con el volumen de fluido contenido en el alabe. Sin embargo, como se justificar´a m´as adelante, en las turbom´aquinas se puede despreciar la contribución de la fuerza de la gravedad al par motor, por lo que ya no lo incluiremos aquí.

Alabe movil 

Suponga ahora el problema del apartado anterior y considere las mismas hipotesis, salvo que, en este caso, el alabe se mueve a velocidad constante →u hacia la derecha con respecto al sistema de referencia fijo a tierra. Considere un volumen de control que incluye alabe, fluido contenido en el y carrito. El volumen de control asi definido se mueve solidario al álabe y sus fronteras están todas a presión atmosférica, para la intersección de la superficie de control con la entrada y salida de fluido son las ´areas S1 y S2, como se ilustra en la figura 2.13. 

La aplicación de la expresión 2.6 al volumen de control descrito con las hip´otesis dadas conduce a: 

Aplicando ahora el teorema de conservación de cantidad de movimiento al volumen de control dado, los términos de la ecuación 2.10 quedan:

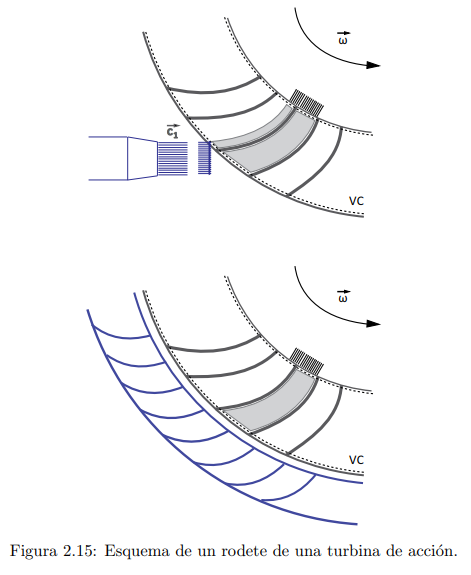
Rueda de alabes 

La acción del flujo sobre el álabe móvil vista en el apartado anterior no tiene sentido práctico, ya que el álabe, en su movimiento de traslación, se aleja indefinidamente de la tobera y el chorro pronto dejaría de incidir sobre aquel. Si en lugar de un alabe desplazándose linealmente, se dispusiera de álabes ubicados en una rueda, siempre habrá uno que sustituya al que se aleja, como se muestra en la figura 2.15. El fluido contenido en la rueda de alabes o rodete, será él volumen de control a considerar y la configuración así formada constituye una turbina de acción.

Como se ha visto en el apartado anterior, las componentes de la fuerza que ejerce el fluido sobre el álabe serán:

Si el rodete está quieto, durante la puesta en marcha, por ejemplo, la fuerza →F por la distancia al eje, es la contribución de ese álabe al par motor. Durante el funcionamiento, la potencia teórica de la turbina de acción vendrá dada por la ecuación 2.25.

Si se sustituye la tobera por una corona fija de álabes, dispuestos de tal forma que cada dos consecutivos formen una tobera, que se alimenta a través de una cámara espiral o caracol, entonces la turbina es de admisión total, es decir, el flujo se distribuye por toda la periferia del rodete (figura 2.16). En este caso, la fuerza →F tiene un término más debido a contribución de las fuerzas de presión sobre las superficies S1 y S2, ya que, al estar inundado el conducto, la distribución de presiones en dichas secciones no tiene por qué ser uniforme e igual a la atmosférica.