FLUIDOS NO NEWTONIANOS
FLUIDOS NO NEWTONIANOS. FUNDAMENTOS
exteriores. La diferencia principal entre sólidos y líquidos viene dada por su reacción ante un esfuerzo. Al aplicar una fuerza en un sólido se produce un cambio en su forma, una deformación finita, y si la fuerza es pequeña el cambio también lo será. En un fluido, si las fuerzas se aplican apropiadamente, por ejemplo como cortadura, el cambio de forma nunca será pequeño, por pequeñas que sean las fuerzas, si estas actúan durante suficiente tiempo, pues lo que se genera es una velocidad de deformación y no una deformación finita. El líquido presenta por lo tanto resistencia a la cizalladura, pues es necesario que se le apliquen esfuerzos cortantes para que se genere una velocidad de deformación, y así si la fuerza es pequeña, la velocidad de deformación también lo será.Según la respuesta que tengan los fluidos ante un esfuerzo cortante, estos pueden clasificarse en newtonianos o no newtonianos. La relación entre esfuerzos cortantes y velocidades de deformación se puede expresar del siguiente modo:
τ = µγ˙ (1.1)
Comportamientos no newtonianos de los fluidos
En los fluidos existen diferentes tipos de comportamientos no newtonianos que se pueden presentar. Chhabra y Richardson (2008) realizan una primera clasificación de los comportamientos no newtonianos a partir de su respuesta temporal, distinguiendo tres categorías:1. Fluidos independientes del tiempo, puramente viscosos o inelásticos. Para los fluidos clasificados en esta categoría, la viscosidad en cualquier instante depende únicamente del esfuerzo cortante en dicho instante.
2. Fluidos dependientes del tiempo. La viscosidad del fluido depende, además del valor del esfuerzo aplicado, de la duración del mismo y su historia cinemática.
3. Fluidos viscoelásticos. Estos fluidos muestran una recuperación parcial elástica tras el cese del esfuerzo cortante.
A su vez, en cada una de las tres categorías se engloban diferentes comportamientos. Para la presente investigación únicamente resultan de interés los comportamientos independientes del tiempo, los cuales se describen en el siguiente apartado.
Es importante constatar que los fluidos reales tendrán a menudo un comportamiento que será combinación de dos o tres comportamientos no newtonianos, aunque siempre se podrá identificar uno de ellos como dominante.
Fluidos independientes del tiempo o inelásticos
El comportamiento de este tipo de fluidos ante esfuerzos cortantes puede describirse por una relación simple del tipo:
γ˙ = Ψ(τ ) (1.2)
Así, dependiendo de la forma que adopte la función Ψ los fluidos independientes del tiempo se puede clasificar en tres subgrupos:
- Dilatantes (Shear-thickening). La viscosidad aparente del fluido aumenta al hacerlo el esfuerzo cortante. Es el comportamiento opuesto al de los fluidos seudoplásticos.
- Seudoplásticos (Shear-thinning). La viscosidad aparente del fluido disminuye al aumentar el esfuerzo cortante al que están sometidos.
- Visco-plásticos o fluidos tipo Bingham. Estos fluidos se caracterizan por un valor límite de esfuerzo tangencial (yield stress), que debe excederse para que el material comience a fluir.
Tal y como se ha comentado, la seudoplasticidad es el tipo más común de comportamiento no newtoniano. Se traduce en una viscosidad aparente que disminuye al aumentar el esfuerzo cortante (véase Fig. 1.1). No obstante, para esfuerzos de cortadura muy bajos o muy elevados, la mayoría de los fluidos seudoplásticos exhiben un comportamiento newtoniano: a valores altos o bajos del esfuerzo cortante, la curva del reograma se hace una recta que pasa por el origen. Ante dichos esfuerzos extremos, se obtienen dos valores de viscosidad: µ0 a esfuerzos muy pequeños y µ∞ a esfuerzos muy grandes. Estos valores dependen de diversos factores, tales como el tipo y concentración del polímero, su distribución de pesos moleculares y la naturaleza del disolvente. Aunque es difícil generalizar, muchos materiales muestran las viscosidades límite inferior y superior para esfuerzos por debajo de 10−2 s −1 y por encima de 105 s −1 , respectivamente.
- Modelo Power Law Es el método más empleado en la literatura relacionada con ingeniería de procesos. Al representar el esfuerzo de cortadura frente a la velocidad de deformación en coordenadas logarítmicas, se obtienen líneas rectas para un rango limitado de esfuerzos (o velocidades de deformación). En este rango, se puede utilizar una ley del tipo:
La caracterización de un fluido como Power Law es muy sencilla, sin embargo tiene algunas desventajas:
- El ajuste lineal se puede aplicar en un rango limitado, y por tanto los coeficientes m y n son solamente válidos en ese rango.
- El modelo no predice los valores de las viscosidades límite µ0 y µ∞.
- Las dimensiones del coeficiente m dependen del valor numérico del coeficiente n. Por tanto, no pueden compararse los valores de distintos coeficientes de consistencia m, cuando los valores n difieren.
Para un flujo laminar a través de un tubo los esfuerzos cortantes que aparecen tienen una distribución como la mostrada en la Fig. 1.3. En el caso de un fluido no newtoniano del tipo Power Law el perfil de velocidades varía en función del parámetro n, siendo más plano para un fluido dilatante (n > 1) y más afilado para un fluido seudoplástico (n < 1), como se muestra en la Fig. 1.4.
El perfil de velocidades de un fluido Power Law en un tubo liso, en caso de que el fluido tenga propiedades homogéneas en toda la sección depende únicamente de la propiedad reológica n. Obviamente el perfil de velocidades será distinto para cada geometría y determinará además la viscosidad aparente del fluido. En el flujo en tubos, el perfil de velocidades viene dado por la siguiente ecuación (la obtención de la misma se detalla en el Apartado 5.1.1):
Por otro lado, los fluidos no newtonianos con más presencia en el mercado son los seudoplásticos, en los que la viscosidad aparente disminuye al aumentar el esfuerzo cortante (Cancela et al., 2005 y Chhabra y Richardson, 2008). Tradicionalmente, no ha habido en la industria tantos fluidos dilatantes (suspensiones concentradas, pastas de almidón) como seudoplásticos, aunque están aumentando debido al creciente interés en el manejo y procesado de sistemas con altas cargas sólidas (Barnes, 1989; Goddard y Bashir, 1990). No hay muchas investigaciones sobre fluidos dilatantes, pero las existentes indican que se ajustan al modelo Power Law con el índice n > 1 (Vincent-Vela et al., 2010; Marn y Ternik, 2006; Ternik et al., 2006; Dhiman, 2009) aunque otros autores proponen modelos más complejos (Galindo-Rosales et al., 2011). La existencia de un yield stress (Barnes, 1999), un umbral de esfuerzo cortante que se debe superar para que el fluido comience a fluir, se da en los fluidos viscoplásticos tales como suspensiones de partículas, emulsiones, productos alimenticios o en la sangre. Hasta hace unos años existían muy pocas publicaciones experimentales sobre fluidos viscoplásticos, aunque han aumentado en los últimos años (Papanastasiou y Boudouvis, 1997; Balmforth et al., 2007; Tokpavi et al., 2008; Afonso et al., 2008).
Uno de los fluidos no newtonianos seudoplásticos que se ajusta de forma adecuada a los requisitos experimentales de la presente investigación (disoluble en agua caliente y fría, transparente en disolución, no tóxica y biodegradable) es la disolución en agua de Carboximetil celulosa (CMC). Pertenece a la familia de los hidrocoloides, que se utilizan para mejorar la consistencia y la textura de productos alimenticios líquidos, semilíquidos y semisólidos. En la industria alimenticia se usa como estabilizador, medio de unión, relleno y para retener agua en galletas, pasteles, helados, zumos, salsas, sopas deshidratadas y productos dietéticos (Pilizota et al., 1996).
El diseño de procesos industriales con fluidos no newtonianos, requiere de datos precisos sobre la reología de los mismos, ya que las características del flujo dependen de la reología y densidad del fluido. Es por ello que existen gran cantidad de publicaciones al respecto. Abdelrahim y Ramaswamy (1995), Ghannam y Esmail (1996), Abu-Jdayil (2003), Cancela et al. (2005), Yang y Zhu (2007) y Benchabane y Bekkour (2008) estudian las propiedades reológicas de las disoluciones de CMC en agua a diferentes concentraciones y temperaturas. Los resultados muestran importantes variaciones en el comportamiento que dependen de la concentración. En concentraciones cercanas al 1 % tiene un comportamiento casi newtoniano que evoluciona a seudoplástico al incrementar la concentración. Además, a concentraciones altas (mayores del 4 %) aparecen efectos viscoelásticos y tixotrópicos. A valores muy bajos velocidades de deformación Benchabane y Bekkour (2008) detectan una zona newtoniana de viscosidad µ0 en disoluciones de concentraciones altas. En la mayor parte del rango de esfuerzos, de acuerdo a los autores el fluido se ajusta correctamente al modelo Power Law.




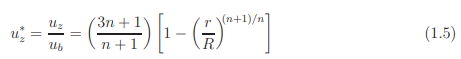

Comentarios
Publicar un comentario