RELACIONES ESFUERZO-DEFORMACIÓN

Existen tres tipos de esfuerzo estáticos a los que se sujetan los materiales: tensión, compresión y cortante. Los esfuerzos de tensión tienden a estirar al material, las de compresión a compactarlo, y las cortantes comprenden tensiones que tienden a ocasionar que porciones adyacentes del material se deslicen una respecto a la otra. La curva esfuerzo-deformación es la relación básica que describe las propiedades mecánicas para los tres tipos.

Propiedades ante la tensión 

La prueba de tensión es el procedimiento más común para estudiar la relación esfuerzo deformación, en particular para los metales. Durante la prueba, se aplica una fuerza que tira del material y tiende a estirarlo y reducir su diámetro, como se ilustra en la figura 3.1a). Los estándares de la ASTM (American Society for Testing and Materials) especifican el modo de preparación del espécimen de prueba y de la realización de la prueba misma. En la figura 3.1b) y c) se ilustran el espécimen común y la preparación general de la prueba, respectivamente. 

El ejemplar con que se inicia la prueba tiene una longitud original Lo y un área Ao . La longitud se mide como la distancia entre las marcas de medición, y el área como la sección transversal (circular, por lo general) del espécimen. Durante la prueba de un metal, el ejemplar se estira, luego le aparece un estrangulamiento y por último se fractura, como se muestra en la figura 3.2. La carga y el cambio de longitud del espécimen se registran conforme la prueba se efectúa a fin de obtener los datos que se requieren para determinar la relación esfuerzo-deformación. Hay dos tipos diferentes de curvas esfuerzo-deformación: 1) la curva de esfuerzo-deformación de ingeniería, y 2) la de esfuerzo-deformación verdadera. La primera es más importante para el diseño, y la segunda lo es para la manufactura. 

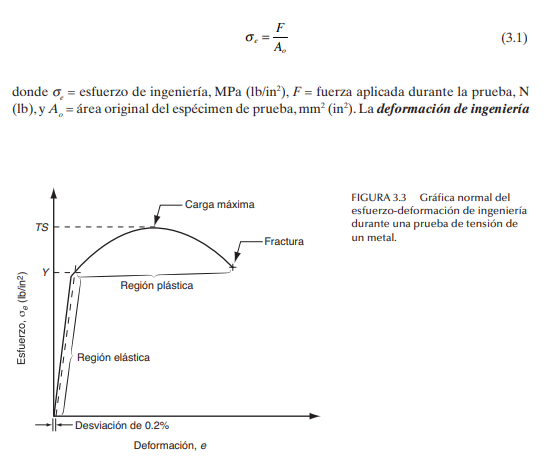
Esfuerzo-deformación de ingeniería El esfuerzo deformación de ingeniería en una prueba de tensión que se define en relación con el área y longitud originales del espécimen de prueba. Dichos valores son de interés en el diseño debido a que el diseñador espera que las tensiones-deformaciones experimentadas por cualquier componente del producto no cambiarán su forma de manera significativa. Los componentes están diseñados para soportar los esfuerzos que se prevé encontrarán durante su uso.

En la figura 3.3 se ilustra una curva común del esfuerzo-deformación de ingeniería de una prueba de tensión de un espécimen metálico. El esfuerzo de ingeniería en cualquier punto de la curva se define como la fuerza dividida entre el área original:

en cualquier punto de la prueba está dada por

donde e = deformación de ingeniería, mm/mm (in/in); L = longitud en cualquier punto durante el estiramiento, mm (in); y Lo = longitud de medición original, mm (in). Las unidades de la deformación de ingeniería se dan como mm/mm (in/in), pero puede concebirse que representan estiramiento por unidad de longitud, sin unidades. 

La relación esfuerzo-deformación de la figura 3.3 tiene dos regiones que indican dos modos distintos de comportamiento: 1) elástico y 2) plástico. En la región elástica, la relación entre el esfuerzo y la deformación es lineal, y el material muestra un comportamiento elástico porque regresa a su longitud original si la carga (esfuerzo) se interrumpe. La relación está definida por la ley de Hooke:

donde E = módulo de elasticidad, MPA (lb/in2 ). E es una medida de la rigidez inherente del material. Es una constante de proporcionalidad cuyo valor es diferente para materiales distintos. En la tabla 3.1 se presentan valores comunes para varios materiales, metales y no metales. 

Conforme el esfuerzo aumenta, se alcanza un punto final en la relación lineal en el que el material comienza a ceder. Ese punto de deformación, Y, del material se identifica en la figura por el cambio de la pendiente al final de la región lineal. Debido a que el comienzo de la deformación por lo general es difícil de ver en una gráfica de datos de prueba (por lo general no ocurre como un cambio abrupto de la pendiente), es común definir a Y como el esfuerzo con el que ocurre un avance de la deformación del 0.2% a partir de la línea recta. En forma más específica, es el punto en el que la curva esfuerzo-deformación del material interseca una recta paralela a la porción recta de la curva, pero desviada de ella por una deformación de 0.2%. 

El punto de deformación es una característica de la resistencia del material, y por ello es frecuente hacer referencia a él como el límite de deformación (otros nombres que recibe son esfuerzo de deformación y límite elástico). El punto de deformación marca la transición hacia la región plástica y el comienzo de la deformación plástica del material. La relación entre el esfuerzo y la deformación ya no estará determinada por la ley de Hooke. Conforme se incrementa la carga más allá del punto de deformación, continúa la elongación del material, pero a una tasa mucho más rápida que la anterior, como se aprecia en la figura 3.3. La elongación va acompañada de una reducción uniforme del área de la sección transversal, consistente con el mantenimiento de un volumen constante. Por último, la carga aplicada F alcanza un valor máximo, y el esfuerzo de ingeniería calculado en ese punto se denomina resistencia a la tensión o resistencia final a la tensión del material. Se denota como TS, donde TS = Fmáx/Ao . TS e Y son propiedades importantes de la resistencia para los cálculos del diseño (también se les usa para hacer los de manufactura). En la tabla 3.2 se enlistan algunos valores comunes de la resistencia a la deformación y resistencia a la tensión para metales seleccionados. Las pruebas convencionales de resistencia a la tensión son difíciles de hacer para las cerámicas, y se emplea una prueba alternativa para medir la resistencia de esos materiales frágiles (véase la sección 3.1.3). Los polímeros difieren de los metales y las cerámicas en sus propiedades de resistencia debido a la plasticidad

A la derecha de la resistencia a la tensión, en la curva esfuerzo-deformación, la carga comienza a declinar y es común que el espécimen de prueba comience un proceso de elongación localizada que se conoce como estrangulamiento. En lugar de continuar la deformación uniforme a todo lo largo de su longitud, comienza a concentrarse la deformación en una sección pequeña del espécimen. El área de esa sección se angosta (se estrangula) de manera significativa hasta que sobreviene la falla. El esfuerzo calculado inmediatamente antes de la falla se conoce como esfuerzo de fractura. 

La cantidad de deformación que el material es capaz de soportar antes de que ocurra la falla también es una propiedad mecánica de interés para muchos procesos de manufactura. La medición común de esta propiedad es la ductilidad, que es la capacidad que tiene un material para deformarse plásticamente sin sufrir una fractura. Esta medición se toma ya sea como elongación o como reducción del área. La elongación se define como

donde EL = elongación, que de manera frecuente se expresa como un porcentaje; Lf = longitud del espécimen al ocurrir la fractura, mm (in), medida como la distancia entre las marcas de medición después de que las dos partes del espécimen se han vuelto a unir; y Lo = longitud original del espécimen, mm (in). La reducción del área se define como

donde AR = reducción del área, que se expresa con frecuencia como porcentaje; Af = área de la sección transversal en el punto de fractura, mm2 (in2 ); y Ao = área original, mm2 (in2 ). Existen problemas con estas dos mediciones de ductilidad debido al estrangulamiento que ocurre en los especímenes de prueba metálicos y el efecto no uniforme asociado con la elongación y la reducción del área. A pesar de esas dificultades, la elongación y la reducción porcentual del área son las medidas de la ductilidad que se emplean con mayor frecuencia en la práctica de la ingeniería. Algunos valores frecuentes del porcentaje de elongación para distintos materiales (sobre todo metales) se enlistan en la tabla 3.3.

Esfuerzo-deformación verdadero Los lectores acuciosos quizás hayan tenido problemas por el uso del área original del espécimen de prueba para calcular los esfuerzos de ingeniería, en lugar del área real (instantánea) que es cada vez más pequeña conforme la prueba avanza. Si se utilizara el área real, los esfuerzos calculados serían mayores. El valor del esfuerzo que se obtiene al dividir la carga aplicada entre el valor instantáneo del área se define como esfuerzo verdadero:

donde s = esfuerzo verdadero, MPa (lb/in2 ); F = fuerza, N(lb); y A = área real (instantánea) que resiste la carga, mm2 (in2 ). 

De manera similar, la deformación verdadera proporciona una evaluación más realista de la elongación “instantánea” por unidad de longitud del material. El valor de la deformación verdadera en una prueba de tensión se estima por medio de dividir la elongación total en incrementos pequeños, el cálculo de la deformación de ingeniería para cada incremento sobre la base de su longitud inicial, y después con la suma de los valores de la deformación. En el límite, la deformación verdadera se define como:

donde L = longitud instantánea en cualquier momento durante la elongación. Al final de la prueba (u otra deformación), el valor final de la deformación se calcula con el uso de L = Lf . 

Cuando se grafican los datos del esfuerzo-deformación de ingeniería de la figura 3.3, con el empleo de los valores del esfuerzo y la deformación verdaderos, la curva que resulta tiene la apariencia de la que se muestra en la figura 3.4. En la región elástica, la gráfica es virtualmente la misma de antes. Los valores de la deformación son pequeños y la deformación verdadera es casi igual a la de ingeniería para la mayor parte de los metales de interés. Los valores de esfuerzo respectivos también están muy cerca el uno del otro. La razón de estas casi igualdades es que el área de la sección transversal del espécimen de prueba no se reduce significativamente en la región elástica. Así, puede utilizarse la ley de Hooke para relacionar el esfuerzo verdadero con la deformación verdadera: s = E.

 La diferencia entre la curva esfuerzo-deformación verdaderos y su contraparte de ingeniería se encuentra en la región plástica. Los valores del esfuerzo son mayores en la región plástica porque en el cálculo ahora se emplea el área instantánea de la sección transversal del espécimen, que se redujo continuamente durante la elongación. Como en la curva anterior, al final ocurre una caída como resultado del estrangulamiento. 

En la figura se utiliza una línea punteada para indicar la continuación proyectada de la gráfica esfuerzodeformación verdaderos, si no hubiera habido estrangulamiento. 

Conforme la deformación se hace significativa en la región plástica, los valores de la deformación verdadera y de ingeniería divergen. La deformación verdadera se relaciona con la correspondiente de ingeniería por medio de 

En la figura 3.4, debe notarse que en la región plástica el esfuerzo se incrementa en forma continua hasta que comienza el estrangulamiento. Cuando esto pasaba en la curva de esfuerzo-deformación de ingeniería, su significancia se perdía porque para calcular el esfuerzo se había utilizado un valor de área que se sabía erróneo. Ahora, cuando el esfuerzo verdadero también se incrementa, no se puede ignorar tan a la ligera. Lo que eso significa es que el metal se está haciendo más fuerte conforme la deformación aumenta. Esta propiedad se denomina endurecimiento por deformación, que se mencionó en el capítulo anterior en el análisis de las estructuras cristalinas, y que tienen casi todos los metales en mayor o menor grado. 

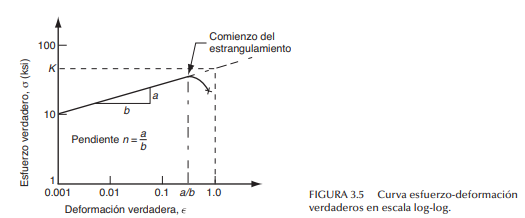
El endurecimiento por deformación, o endurecimiento por trabajo, como se le denomina con frecuencia, es un factor importante en ciertos procesos de manufactura, en particular en la laminacion del metal. Ahora se examinará el comportamiento de un metal en función de cómo lo afecta esta propiedad. Si la parte de la curva esfuerzo-deformación verdaderos que representa la región plástica se graficara en una escala log-log, el resultado sería una relación lineal, como se aprecia en la figura 3.5. Debido a que con esta transformación de los datos se genera una línea recta, la relación entre el esfuerzo verdadero y la deformación verdadera en la región plástica se expresa como

Esta ecuación se llama curva de flujo, y proporciona una aproximación buena del comportamiento de los metales en la región plástica, inclusive de su capacidad de endurecerse por deformación. La constante K se llama coeficiente de resistencia, MPa (lb/in2 ), y es igual al valor del esfuerzo verdadero para un valor igual a 1 de la deformación verdadera. El parámetro n se denomina exponente de endurecimiento por deformación, y es la pendiente de la recta que se observa en la figura 3.5. 

Su valor está directamente relacionado con la tendencia de un metal para endurecerse con el trabajo. En la tabla 3.4 se dan valores comunes de K y n para metales seleccionados. 

El estrangulamiento en una prueba de tensión y en operaciones de laminado de metales que estiran la pieza de trabajo se relaciona estrechamente con el endurecimiento por deformación. Ahora se estudiará esta relación según se observa durante una prueba de tensión. Conforme el espécimen de prueba se estira durante la parte inicial de la prueba (antes de que comience el estrangulamiento), ocurre una deformación uniforme en toda la longitud porque si cualquier elemento de la muestra se deformara más que el metal circundante, su resistencia aumentaría debido al endurecimiento por trabajo, lo que lo haría más resistente ante una deformación adicional y hasta que el metal vecino se hubiera deformado una cantidad igual. Por último, la deformación se hace tan grande que no puede sostenerse en forma uniforme. Se desarrolla un punto débil de la longitud (debido a la formación de dislocaciones en las fronteras de los granos, impurezas del metal, u otros factores), y comienza el estrangulamiento, lo que conduce a la falla. Las evidencias empíricas revelan que el estrangulamiento comienza para un metal en particular cuando la deformación verdadera alcanza un valor igual al exponente de endurecimiento por deformación, n. Por tanto, un valor elevado de n significa que el metal puede deformarse todavía más antes del comienzo del estrangulamiento durante la carga de tensión. 

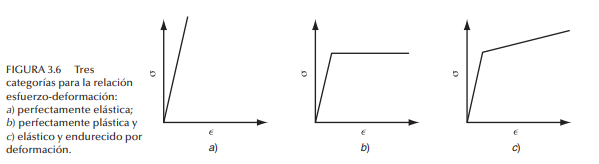
Tipos de relaciones esfuerzo-deformación La curva de esfuerzo-deformación verdaderos proporciona mucha información sobre el comportamiento elástico-plástico. Como se dijo, la ley de Hooke (σ = Ee) gobierna el comportamiento del metal en la región elástica, y la curva de flujo (σ Kn ) lo determina en la región plástica. Son tres las formas básicas de relación esfuerzo-deformación que describen el comportamiento de casi todos los materiales sólidos, las que se muestran en la figura 3.6:

a) Perfectamente elástico. El comportamiento de este material queda definido por completo por su rigidez, indicada por el módulo de elasticidad E. En lugar de producir un flujo plástico, se fractura. Los materiales frágiles tales como las cerámicas, muchos tipos de hierro colado y polímeros termoestables, poseen curvas de esfuerzo-deformación que pertenecen a esta categoría. Estos materiales no son buenos candidatos para las operaciones de laminado. 

b) Elástico y perfectamente plástico. Este material tiene una rigidez definida por E. Una vez que se alcanza la resistencia de deformación, Y, el material se deforma plásticamente con el mismo nivel de esfuerzo. La curva de flujo está dada por K = Y, y n = 0. Los metales se comportan de esta manera cuando se calientan a temperaturas suficientemente altas que los recristalizan en lugar de endurecerlos por deformación durante su trabajo. El plomo presenta este comportamiento a temperatura ambiente porque ésta es superior al punto de recristalización del plomo. 

c) Elástico y endurecimiento por deformación. Este material obedece a la ley de Hooke en la región elástica. Comienza a fluir a su resistencia de deformacion Y. Una deformación continua requiere un esfuerzo siempre incremental, dada por una curva de flujo cuyo coeficiente de resistencia K es mayor que Y y cuyo exponente de endurecimiento por deformación, n, es mayor que cero. La curva de flujo por lo general se representa como función lineal en una gráfica hecha en papel logarítmico. La mayor parte de metales dúctiles se comportan de este modo cuando se trabajan en frío. 

Los procesos de manufactura que deforman los materiales a través de la aplicación de esfuerzos de tensión que incluyen el estirado de alambres y barras.

Propiedades ante la compresión

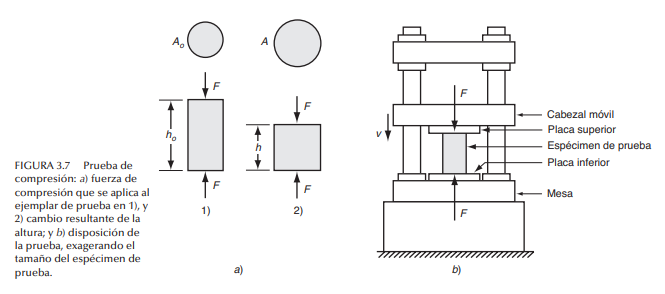
Una prueba de compresión aplica una carga que comprime una muestra cilíndrica colocada entre dos placas, como se ilustra en la figura 3.7. Conforme se comprime, su altura se reduce y el área de su sección transversal se incrementa. El esfuerzo de ingeniería se define como

donde Ao = área original del espécimen. Ésta es la misma definición del esfuerzo de ingeniería que se utilizó en la prueba de tensión. La deformación de ingeniería se define como

donde h = altura del espécimen en un momento particular de la prueba, mm (in); y h0 = altura inicial, mm (in). Debido a que durante la compresión la altura disminuye, el valor de e será negativo. El signo negativo por lo general se ignora cuando se expresan los valores de la deformación por compresión. 

Si en una prueba de compresión se grafica el esfuerzo de ingeniería contra la deformación de ingeniería, el resultado se asemeja a la figura 3.8. Como antes, la curva se divide en las regiones elástica y plástica, pero la forma de la parte plástica es diferente de aquella correspondiente a la prueba de tensión. Debido a que la compresión ocasiona que la sección transversal se incremente (en vez de disminuir, como en la prueba de tensión), la carga se incrementa con mayor rapidez que antes. Esto da como resultado un valor más alto del esfuerzo de ingeniería calculado. 

En la prueba de compresión ocurre algo más que contribuye al aumento del esfuerzo. Conforme el espécimen cilíndrico se comprime, la fricción en sus superficies que están en contacto con las placas tiende a impedir que los extremos del cilindro se expandan. Durante la prueba se consume energía adicional debido a esta fricción, lo que da como resultado una fuerza aplicada más grande. También se muestra un incremento en el esfuerzo de ingeniería calculado. Así, debido al aumento del área de la sección transversal y a la fricción entre el espécimen y las placas, se obtiene la curva esfuerzo-deformación de ingeniería característica de una prueba de este tipo según se aprecia en la figura

Otra consecuencia de la fricción entre las superficies es que el material cercano de la parte media del espécimen sí puede incrementar su área mucho más que los extremos. Esto resulta en que la muestra adopte una forma característica de barril, como se ilustra en la figura 3.9. 

Aunque hay diferencias entre las curvas de esfuerzo-deformación de ingeniería correspondientes a la tensión y a la compresión, cuando se grafican los datos respectivos como esfuerzo-deformación verdaderos, las relaciones son casi idénticas (para casi todos los materiales). Debido a que en la bibliografía abundan más los resultados de la prueba de tensión, es posible obtener valores de los parámetros de la curva de flujo (K y n) a partir de datos de esas pruebas y aplicarlos con igual validez a una operación de compresión. Lo que debe hacerse al usar los resultados de la prueba de tensión para una operación de compresión es ignorar el efecto de la estrangulación, fenómeno que es peculiar para la deformación inducida por esfuerzos de tensión. En la compresión no hay un colapso correspondiente del trabajo. (Podría argumentarse que el abombamiento de secciones largas y delgadas durante la compresión es la contraparte del estrangulamiento. Sin embargo, ese abombamiento es un modo de falla que involucra la flexión del espécimen, por lo que el esfuerzo ya no se limita sólo a la compresión. En la sección siguiente se estudian los esfuerzos del doblado.) En las gráficas anteriores de curvas de tensión de esfuerzo-deformación se extendieron los datos más allá del punto de estrangulamiento por medio de líneas punteadas. Éstas representan mejor el comportamiento del material durante la compresión que los datos de prueba reales de la tensión. 

Las operaciones de compresión en la forja de metal son mucho más comunes que las de estiramiento. Los procesos importantes de compresión en la industria incluyen el laminado, forjado y extrusión.

Doblado y prueba de materiales frágiles 

Las operaciones de doblado se emplean para formar placas y hojas metálicas. Como se ve en la figura 3.10, el proceso de doblar una sección transversal rectangular, sujeta al material a esfuerzos de tensión (y deformación) en la mitad externa de la sección que se dobla, y a esfuerzos de compresión (y deformaciones) en la mitad interior. Si el material no se fractura, queda doblado en forma permanente (plásticamente), como se muestra en el inciso 3) de la figura 3.10.

Los materiales duros y frágiles (por ejemplo, cerámicas), que tienen elasticidad pero poca o ninguna plasticidad, con frecuencia se prueban con un método que sujeta a la muestra a una carga flexionante. Estos materiales no responden bien a las pruebas de tensión tradicionales debido a los problemas para preparar los especímenes de prueba y la posibilidad de alinear mal las partes de la prensa que los sujeta. La prueba de doblado (también conocida como prueba de flexión) se utiliza para probar la resistencia de estos materiales, con el uso del arreglo que se ilustra en el primer diagrama de la figura 3.10. En ese procedimiento, se coloca un espécimen de sección transversal rectangular entre dos apoyos, y en su centro se aplica una carga. En esta configuración, la prueba se denomina de doblado de tres puntos. En ocasiones también se utiliza una configuración de cuatro puntos. Los materiales frágiles no se flexionan en el grado exagerado que se muestra en la figura 3.10; en vez de ello, se deforman elásticamente hasta el momento inmediato anterior a la fractura. La falla ocurre por lo general porque se excede la resistencia final de tensión de las fibras exteriores del espécimen. Esto da como resultado un agrietamiento o clivaje, modo de falla que se asocia con las cerámicas y metales que operan a temperaturas de uso bajas, en el que en vez de separación ocurre deslizamiento a lo largo de los planos cristalográficos. El valor de resistencia obtenido de esta prueba se denomina resistencia a la ruptura transversal, y se calcula con la fórmula siguiente

donde TRS = resistencia a la ruptura transversal, MPa (lb/in2 ); F = carga aplicada al ocurrir la fractura, N (lb); L = longitud entre los apoyos del espécimen, mm (in); y b y t son las dimensiones de la sección transversal del espécimen, como se muestra en la figura, mm (in). La prueba de flexión también se utiliza para ciertos materiales que no son frágiles, tales como los polímeros termoplásticos. En este caso, como es probable que el material se deforme en vez de fracturarse, no puede determinarse la TRS con base en la falla del espécimen. En vez de ello, se emplea cualquiera de dos medidas: 1) la carga registrada para un nivel dado de deflexión, o 2) la deflexión observada para una carga dada.

Propiedades ante la cortante 

Una cortante comprende la aplicación de esfuerzos en direcciones opuestas sobre ambos lados de un elemento delgado a fin de deformarlo como se muestra en la figura 3.11. El esfuerzo cortante se identifica como 

donde t = esfuerzo cortante, lb/in2 (MPa); F = fuerza aplicada, N (lb); y A = área sobre la que se aplica la fuerza, in2 (mm2 ). La deformación cortante se define como

donde g = deformación cortante, mm/mm (in/in); d = deflexión del elemento, mm (in); y b = distancia ortogonal sobre la que ocurre la deflexión, mm (in). Es común probar el esfuerzo y deformación cortantes por medio de una prueba de torsión, en la que un espécimen tubular de pared delgada se sujeta a un par, como se ilustra en la figura 3.12. Conforme el par aumenta, el tubo se flexiona por torsión, que para esta geometría es una deformación cortante. 

En la prueba, el esfuerzo cortante se determina con la ecuación

donde T = par aplicado, N-mm (lb-in); R = radio del tubo medido respecto del eje neutro de la pared, mm (in); y t = espesor de la pared, mm (in). La deformación cortante se determina con la medición de la cantidad de deflexión angular del tubo, la que se convierte a distancia flexionada y se divide entre la longitud de medición, L. Al reducir esto a una expresión sencilla queda

donde a = la deflexión angular (radianes).

En la figura 3.13 se presenta una curva común de esfuerzo-deformación cortante. En la región elástica, la relación está definida por

donde G = módulo de la cortante, o módulo de la cortante de elasticidad, MPa (lb/in2 ). Para la mayoría de los materiales, el módulo de la cortante es aproximadamente de G = 0.4E, donde E es el módulo de elasticidad convencional. 

En la región plástica de la curva esfuerzo-deformación cortante, el material sujeto a deformación se endurece y ocasiona que el par aplicado aumente hasta que, finalmente, ocurre la fractura. En esta región, la relación es similar a la curva de flujo. Es posible calcular el esfuerzo cortante en la fractura, que se usa como la resistencia a la cortante, S, del material. La resistencia a la cortante se puede estimar a partir de los datos de resistencia a la tensión, por medio de la aproximación: S = 0.7(TS). 

Como el área de la sección transversal del espécimen en la prueba de torsión no cambia, como sí lo hace en las pruebas de tensión y compresión, la curva de esfuerzo-deformación de ingeniería para la cortante obtenida a partir de la prueba de torsión es virtualmente la misma que la curva esfuerzo-deformación verdadera. 

En la industria son comunes los procesos cortantes. La acción cortante se utiliza para cortar láminas metálicas en operaciones de cizallado, punzonado y otras (véase la sección 20.1). Al maquinar, el material se retira por medio del mecanismo de deformación cortante