La velocidad de propagación del sonido
Ondas sonoras
Las ondas se clasifican en función de diferentes características.
En el sentido de la vibración, esto es en ondas transversales y ondas
longitudinales (ver figura 2.1). En una onda transversal, la vibración es
perpendicular a la dirección de propagación, la onda en el agua, es un ejemplo
de onda transversal, ya que la onda se desplaza en la dirección paralela a la
superficie del agua, pero hace oscilar el medio arriba y abajo. En una onda longitudinal,
la vibración es en la misma dirección que la de propagación [26]. Las ondas
sonoras son un tipo de onda longitudinal, donde las partículas del medio se
mueven hacia adelante y hacia atrás y crean zonas de mayor o menor densidad
como resultado de variaciones de presión de un punto a otro punto a través de
cualquier medio material, sea sólido, líquido o gas (ver figura 2.2). Además,
se propagan con una velocidad específica para cada medio la cual depende de las
propiedades de dicho medio que experimenta la perturbación. Así, en un líquido
la velocidad es mayor que en un gas y en un sólido es mayor que en un líquido
[28].
Características cuantitativas y cualitativas
Las diversas medidas cuantitativas necesarias para describir una onda son: fase, frecuencia, periodo, velocidad de propagación, longitud de onda y número de onda. La frecuencia f es el número de oscilaciones en una unidad de tiempo. Por el contrario, el tiempo necesario para que se lleve a cabo una oscilación es el periodo, T, por lo tanto, T = 1/f. Las unidades de frecuencia son múltiplos del Hertz (Hz). Un Hertz es el número de oscilaciones que hay en un segundo (ciclos por segundo). La longitud de onda λ, es la distancia que hay entre el mismo punto de dos ondulaciones consecutivas. Por el contrario, el número de ciclos en una distancia es 1/λ, y el número de onda k es el número de radianes en un ciclo, k = 2π/λ [29].
El progreso de una onda es descrito por una velocidad de onda c (´o velocidad del sonido en el caso de una onda sonora). La velocidad de onda depende del material y, excepto para materiales isotrópicos, es decir, materiales que presentan las mismas propiedades físicas en todas direcciones, esta depende también de la dirección de propagación. Para los fines de este trabajo de tesis se considera que todos los gases y líquidos son isótropos, ya que de no ser así el problema a resolver se complica considerando otros parámetros como la estructura molecular de la materia, por lo cual, si se considera un fluido ideal, la velocidad de onda depende únicamente del material [8]. La fase total, temporal y espacial de una onda que se propaga es: ϕ = kg − tú = k (x − co), donde c = ω/k = fe, la velocidad de onda, así la fase indica la situación instantánea en el ciclo de la onda. La velocidad de onda se determina por las fuerzas de la elasticidad e inercia propias del material [29].
La velocidad de propagación del sonido varía dependiendo del tipo y características del material por el que atraviese. También varía con la temperatura ya que esta interviene con la energía interna del sistema, ya que un aumento de energía interna debido al aumento de la temperatura favorece la interacción entre las moléculas y de este modo la propagación de energía que lleva la onda de sonido [17], [26]. Otros factores, además de la temperatura, que determinan la velocidad del sonido a través de una sustancia son la densidad y la compresibilidad [28]. Estos dos términos se refieren a la cantidad y distancia de las moléculas, respectivamente, por lo que la velocidad es inversamente proporcional a la compresibilidad, es decir, las moléculas en los medios más compresibles están muy separadas, por lo que trasmiten el sonido más lentamente, por lo tanto, los materiales con mayor densidad y menor compresibilidad transmitirán el sonido a una mayor velocidad [29].
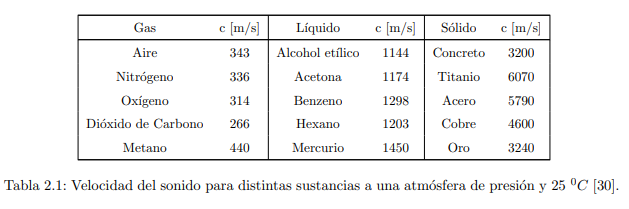
Para tener una idea de los valores aproximados de la velocidad del sonido c en las sustancias, la velocidad del sonido en el aire a temperatura ambiente y presión atmosférica es de aproximadamente 340 m/s. En una sustancia líquida, la velocidad es de alrededor de 1200 m/s y en un sólido de 5000 m/s (como lo muestra la tabla 2.1) a temperatura ambiente. La velocidad del sonido en un sólido depende en una muy pequeña proporción de la temperatura, menos del 10 o 15 % desde la temperatura cero hasta casi su punto de fusión, algo que no pasa con los gases [28].
Hay parámetros físicos que influyen en la propagación de las ondas tales como: dispersión del haz o atenuación geométrica, energía de absorción o atenuación del material y reflexión. La atenuación geométrica es causada por la dispersión de la onda debido a su fuente que es de tamaño finito como lo es un transductor [29]. Una fuente típicamente produce un haz cónico, en el cual el Angulo de divergencia se determina por el tamaño del transductor y la longitud de onda, es por eso la importancia de seleccionar una frecuencia de excitación adecuada en los experimentos y asegurar de este modo una onda plana. Esta atenuación cambia la energía contenida de una onda, pero no la velocidad o la forma de la onda [29]. La atenuación del material ocurre debido a interacciones de fricción internas, la cual convierte la energía cinética en calor. Estos son procesos moleculares como viscosidad y plasticidad, también como respuesta de la estructura del material. La reflexión sucede cuando el sonido se encuentra con un obstáculo, lo que hace la mayor parte de la energía de la onda, es cambiar de fase y volver por el mismo camino por el que ha llegado, pero en sentido contrario [29].
La variación de c con la frecuencia y la dispersión, es pequeña. En los sólidos es usualmente menor al 1 % [28]. En los fluidos es raramente mayor que el 25 %, excepto en el caso de un gas ya que es más sensible. En contraste a la velocidad, la absorción es altamente dependiente de la frecuencia y la temperatura [28]. Por ejemplo, una onda plana de sonido de frecuencia 103 Hz puede viajar cientos de metros sin una atenuación apreciable en su intensidad, pero en el caso de que la propagación sea en un gas a una frecuencia arriba de 1 MHz su intensidad es en general apenas medible después de 10 cm, y en un líquido o en un sólido arriba de 50 MHz. La longitud de onda a estas frecuencias es 0.03 cm en un gas, 0.002 cm en un líquido, y 0.01 cm en un sólido respectivamente [28]. Esta es la fuerte dependencia de la frecuencia con la absorción, además con el hecho de que, en un proceso físico dado, usualmente contribuye significantemente a el solo en una frecuencia particular y un rango de temperaturas que ha hecho que los estudios de absorción sean muy importantes para la investigación acerca de las propiedades físicas de la materia [20].
Técnicas experimentales de mediciones ultrasónicas
La producción de vibraciones ultrasónicas son generalmente efectuadas con la ayuda de cristales piezoeléctricos, de los cuales el cuarzo es usualmente preferido por su alta resistencia mecánica. Una placa de cuarzo puede hacer vibraciones en uno de sus modos de vibración mediante la aplicación de un campo eléctrico alternante con una frecuencia apropiada a lo largo de la dirección determinada, y es así como el dispositivo produce las ondas, a este dispositivo se le conoce como transductor [29]. De este modo, un transductor se define como un dispositivo capaz de transformar o convertir un determinado tipo de energía de entrada en otra de diferente a la salida.Los métodos que hacen uso de las ondas de ultrasonido, las cuales tienen frecuencias arriba de 20KHz como lo muestra la figura 2.3 han sido usados extensivamente en diversas áreas como en electrónica avanzada [29]. Algunas de las aplicaciones más comunes son en la industria, por ejemplo, en inspección de defectos en partes industriales, detección de porosidades, hoyos, irregularidades y hasta composiciones de material. La velocidad de propagación de una onda, proporciona características específicas del objeto de estudio sobre el que se propague el sonido la cual se puede medir con gran precisión, limitándose solamente por características tecnológicas como por ejemplo el tiempo de respuesta del sistema de transductores que se use.
Los métodos experimentales utilizados en la determinación de la velocidad del sonido en un medio, se pueden clasificar en tres grandes grupos [8]:
- El método interferómetro el cual es apropiado para líquidos y gases, por debajo de 1 MHz de frecuencia.
- El método óptico, el cual es apropiado para líquidos y gases.
- El método de pulsos, apropiados para líquidos y sólidos.
Método interferómetro
El método interferómetro es regularmente más usado en la medición de la velocidad del sonido en gases y si este se encuentra a muy bajas densidades es el único método práctico. Aunque también es útil en líquidos. Este método consiste en un transductor el cual es excitado con lo que se genera una onda plana la cual viaja a través del fluido hasta un reflector de plano que es mantenido paralelo al transductor y que puede ser desplazado normalmente a lo largo de la dirección del haz sonoro. Cuando la distancia entre el transductor y el reflector es un número entero de semilongitudes de ondas, se establece una onda estacionaria en la columna del fluido [8].
La onda reflejada que regresa a la superficie del cristal del transductor está entonces desfasada 180 grados con el movimiento del cristal, resultando en una disminución de la amplitud de la oscilación lo cual esta acompañado de una disminución de la corriente alterna que pasa por el cristal del transductor. Si se hace la medición de la corriente en el cristal, que presenta estrechos mínimos, y si se determina la distancia recorrida por el reflector entre sucesivos mínimos se puede obtener directamente el tamaño de la semilongitudes de onda sonora a la frecuencia del oscilador. De estas dos mediciones, se puede calcular la velocidad del sonido [8]. Como muchos experimentos que se realizan en el laboratorio, este método presenta dificultades técnicas, como la perdida de paralelismo entre el transductor y reflector lo que causa perdida de precisión en la medición de la velocidad por las variaciones mínimas de corriente que se miden.
Método óptico
El método óptico depende del hecho de que cuando una onda de sonido pasa a través de un medio produce alternativamente regiones de rarefacción y compresión en el cual entonces actúa sustancialmente como una rejilla de difracción [8]. Las regiones densas en las que gran número de moléculas se agrupan acercándose mucho entre sí se llaman compresiones. Una compresión corresponde a una región de alta presión. Las regiones que tienen relativamente pocas moléculas se conocen como rarefacciones y corresponden a zonas de baja presión (ver figura 2.4).
A partir de los ángulos en los que diversos ordenes difractados aparecen se obtiene la longitud de onda. La intensidad de un orden dado depende entre otras cosas de la amplitud de la onda de sonido, y por mediciones de su intensidad en patrones de difracción a diferentes distancias de la fuente es posible obtener el coeficiente de absorción [29]. Las intensidades de las lıneas difractadas en los gases son considerablemente mas débiles que en lıquidos, por lo que este método es raramente usado en gases a menos que sea usada una onda de sonido muy intensa. El método óptico ha sido usado ampliamente para medir la velocidad de sonido de ondas supersónicas en lıquidos [29].
Método de pulsos
En ambas técnicas la energía ultrasónica es transmitida continuamente al medio. En la primera técnica, solo se hace una corta transmisión, es decir, la transmisión del cristal de cuarzo está siendo conducida por pulsos de corriente alterna de duración tan solo de unos cuantos segundos [7]. Un transductor similar colocado al final del otro lado del medio actúa como un receptor el cual transforma de vuelta el pulso ultrasónico en un pulso de corriente alterna. La medición del tiempo de llegada del pulso ultrasónico en el receptor determina la velocidad, mientras que de la corriente inducida en ´él se determina la absorción. En el método de pulso-eco, el transductor receptor es remplazado por la pared del contenedor de la muestra y el mismo transmisor de la onda actúa como un receptor de la onda reflejada (ver figura 2.5). Una vez que el pulso emitido es detectado se determina el tiempo que tardó en ser registrado, entonces la velocidad se determina como la distancia sobre el tiempo registrado [4].
- El pulso ultrasónico contenga muchas ondas sinusoidales.
- La distancia entre los dos transductores sea grande comparada con la longitud del pulso ultrasónico.
- La distancia entre los dos transductores no debe ser tan grande comparado con el pulso ultrasónico para que la respuesta no sea muy débil en el receptor.
El coeficiente de absorci´on de las ondas planas con que se trabaja y la velocidad de la onda depende de su frecuencia y de la naturaleza del medio solamente, y son independientes de la amplitud de la onda y de la geometría del recipiente en el caso de un fluido o la forma en caso de un s´olido. Esto hace que la interpretación de los resultados sea sencilla y también mantiene los calculos teoricos en un m´ınimo. La condición para la obtención de una onda plana es que las dimensiones lineales de la secci´on transversal del transductor y del medio en contacto con el, se encuentren normales a la direcci´on de propagaci´on, y que esta sea grande comparada con la longitud de onda de dicha onda [29].






Muchas gracias por la información, me fue de mucha utilidad.
ResponderEliminar