SIGNIFICANCIA ESTADÍSTICA DE LAS PROPIEDADES DE LOS MATERIALES

En las ideas que se presentaron en la sección anterior existe un punto fino que debe ponderarse antes de continuar. En la figura 2-2 se muestra el resultado de una sola prueba de tensión (una probeta, ahora fracturada). Por lo general, los ingenieros consideran estos valores importantes del esfuerzo (en los puntos pl, el, y, u y f) como propiedades y los denotan como resistencias con una notación especial, S mayúscula, en lugar de la sigma minúscula , con subíndices agregados: Spl para el límite de proporcionalidad, Sy para la resistencia a la fluencia, Su para la resistencia última a la tensión (Sut o Suc, si el sentido de tensión o compresión es importante). 

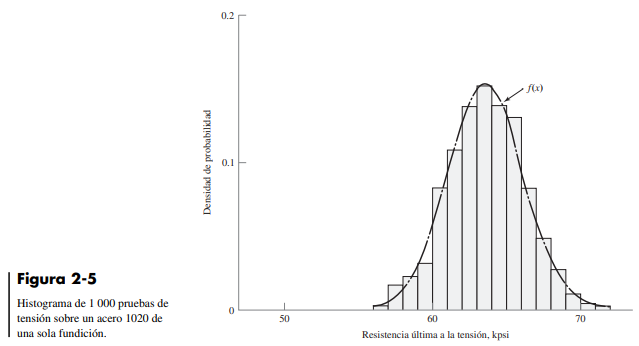
Si hubiera 1 000 piezas nominalmente idénticas, los valores que se obtendrían para la resistencia estarían distribuidos entre algunos valores máximos y mínimos. Se deduce que la descripción de la resistencia, una propiedad del material, tiene una distribución y, por lo tanto, es de naturaleza estadística. En el capítulo 20 se proporcionan más detalles sobre las consideraciones estadísticas involucradas en el diseño. Aquí simplemente se describen los resulta dos de un ejemplo, ejercicio 20-4. Observe la siguiente tabla, que es un reporte histográfico que contiene los esfuerzos máximos de 1 000 pruebas de tensión en un acero 1020 de una sola fundición. Aquí se trata de determinar la resistencia última a la tensión Sut. La frecuencia de cla - se es el número de ocurrencias dentro de un rango de 1 kpsi dado por el punto medio de la clase. Así, ocurrieron 18 valores de esfuerzo máximo en el rango entre 57 y 58 kpsi.

La densidad de probabilidad se define como el número de ocurrencias dividido entre el número total de muestras. En la gráfica de barras de la figura 2-5 se muestra el histograma de la densidad de probabilidad. Si los datos están en la forma de una distribución gaussiana o normal, la función de densidad de probabilidad determinada en el ejemplo 20-4 es

donde el esfuerzo medio es 63.62 kpsi y la desviación estándar es 2.594 kpsi. En la figura 2-5 se incluye una gráfica de f(x). En consecuencia, la descripción de la resistencia Sut se expresa en términos de sus parámetros estadísticos y su tipo de distribución. En este caso Sut N(63.62, 2.594) kpsi, lo que indica una distribución normal con un esfuerzo medio de 63.62 kpsi y una desviación estándar de 2.594 kpsi. 

Observe que el programa de pruebas ha descrito la propiedad Sut del 1020, para una sola fundición de un proveedor. Las pruebas implican un proceso complejo y caro. A menudo, las tablas de propiedades se preparan para ser utilizadas por otras personas. Una cantidad estadística está descrita por su media, su desviación estándar y su tipo de distribución. Muchas tablas

representan un solo número, que frecuentemente es la media, el mínimo o algún percentil, como el percentil 99. Siempre lea las notas al pie de la tabla. Si no se hace una descripción de una tabla con una sola entrada, toda ella está sujeta a serias dudas. Como no es sorprendente que las descripciones de una propiedad sean estadísticas por naturaleza, los ingenieros, cuando ordenan pruebas de propiedades, deben girar instrucciones de manera que los datos generados sean suficientes para observar los parámetros estadísticos e identificar las características de su distribución. El programa de pruebas de tensión sobre 1 000 piezas de acero 1020 es muy grande. Si usted tuviera la necesidad de poner algo en una tabla de resistencias últimas a la tensión y estuviera restringido a un solo número, ¿cuál sería este?, y ¿cuál sería su nota al pie de la tabla?